| デルタ関数δ(t)の最大値は∞ですが、Excelにおいて振幅は有限なのでそんな値はとることができません。 ここでは最大値を1に制限したデルタ関数d[t]を使います。 定義は ・d[0]=1 ・(それ以外)=0 です。 ここで、ある関数g(t)をフーリエ変換したとき、その操作、変換後のg(t)をそれぞれ F[g(t)]=g~(f) と書くことにします。 |
|
 Zoom Zoom |
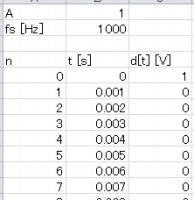
パラメータを用意します。 ・fs:サンプリング周波数 ・n:サンプル番号(0からスタートを推奨) ・t:時間 [s] ・d[t]:制限デルタ関数 [V] サンプリング周波数は0以外の適当な数値を入れてください。 tのアキュムレータの構成方法は自由です。 d[t]は上に書いた通りです。 それぞれ、128個以上用意しましょう。 |
 Zoom Zoom |
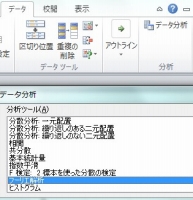
データが用意できたところで、DFTを行います。 DFT機能は データ→解析→フーリエ解析 から選択できます。 |
 Zoom Zoom |
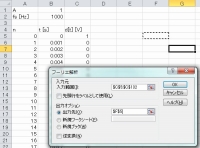
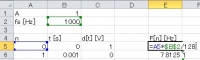
パラメータを入力するウインドウが出ます。 入力範囲はd[t]の0サンプル〜127サンプルを選択します。 FFTの構造上、2^n個の範囲しか選ぶことができません。 この選択範囲(変換範囲)を「窓、ウインドウ」と言い、窓に収まるデータ個数(窓の大きさ)の単位は普通「ポイント、pts」と表されます。 したがって、今回は128 ptsのFFTです。 出力は「出力先」ボタンを選択し、時間領域信号部分から少し離れた場所を指定します。 設定が完了したら、「OK」をクリックしましょう。 |
 Zoom Zoom |
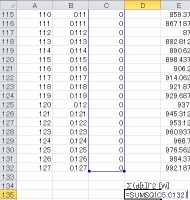
エラーの付いたセルが128個できるはずです。 エラーは「数字が文字列として書かれている」というものなので、無視してもかまいません。 結果を見ると、すべて同じ値になっているはずです。 ですが、各成分に対応する周波数がありません。 出力の一番上を0番目としたn番目の周波数をF[n] [Hz]、窓の大きさをL[pts]として F[n]=n*fs/L と書けます。 |
| よく見ると結果はすべて実数です。 連続時間領域でデルタ関数をフーリエ変換すると δ~(f)=exp(-i*2πf*0)=cos(-2πf*0)+i*sin(-2πf*0)=1 すなわち、周波数にかかわらず実数で一定です。 DFTの結果はこれの定数倍であり、離散信号においてもフーリエ変換が成立することが分かります。 |
|
| フーリエ変換の出力は必ず複素数なので、それに対応した出力となっています。 Excelでの複素数は「(実数)±(虚数)i」で表記します。 もちろん、Excelには複素数に対応した関数が用意されています。 |
|
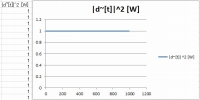
| 直交座標だと分かりにくいので、周波数成分の電力を示す「パワースペクトル」に直しましょう。 電力は電圧の2乗に比例するので、複素数の絶対値を2乗します。 Excelの関数で複素数の絶対値はIMABS()で求められます。 変換後のd[t]をd~[f] [Hz]、パワースペクトルを|d~[f]|^2 [W]と置くと |d~[f]|^2=IMABS(d~[f])^2 と書けます。 |
|
 Zoom Zoom |
結果は定数なので面白くありませんが、グラフ化してみましょう。 ナイキストのサンプリング定理より、ナイキスト周波数以上のスペクトルは利用できません。 今回は関数の性質上確認できませんが、DFTのパワースペクトルはナイキスト周波数を軸に左右対称になります。 正確に言うと、複素スペクトルにおいて複素共役になっており、逆相、すなわち負周波数のスペクトルを示しています。 |
| 余談: ちなみに極座標の位相を求めるにはIMARGUMENT()です。 もちろん角度の単位はラジアンです。 |
|
| 余談2: フーリエ変換が可逆変換であることは周知のとおりです。 先ほどのパラメータ指定ウインドウで気づいたかもしれませんが、ExcelのDFTも可逆変換です。 気になる方は線スペクトルなど、時間領域に変換して確かめてみてください。 |
 Zoom
Zoom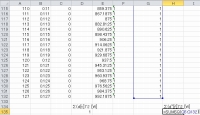 Zoom
Zoom